BSDF (Bidirectional Scattering Distribution Function)

1. What is BSDF?

The BSDF (bidirectional scattering distribution function) is a superset and the generalization of the BRDF and BTDF.

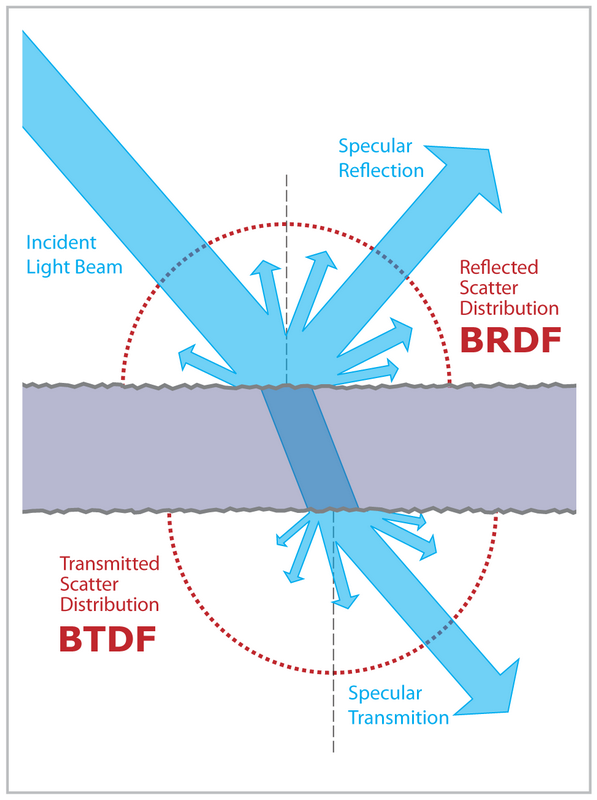
BSDF (Image source: Wikipedia)

1.1 The BRDF

The BRDF (bidirectional reflectance distribution function) $f_r(p, \omega_o, \omega_i)$ is a function over pairs of directions $\omega_i$ and $\omega_o$ that describes how much incident light along $\omega_i$ is scattered from the surface in the direction $\omega_o$ at one point.

BRDF (Image source: PBRT)

Given an incident radiance along the direction $\omega_i$, $L_i(p, \omega_i)$, the BRDF computes how much radiance is leaving the surface in the direction $\omega_o$ toward the viewer $L_o(p, \omega_o)$:

\[f_r(p, \omega_o, \omega_i) = \frac{dL_o(p, \omega_o)}{L_i(p, \omega_i)cos\theta_i d\omega_i}\]

1.2 The BTDF

The BTDF (bidirectional transmittance distribution function), which describes the distribution of transmitted light, can be defined in a manner similar to that for the BRDF. The BTDF is generally denoted by $f_t(p, \omega_o, \omega_i)$, where $\omega_i$ and $\omega_o$ are in opposite hemispheres around $p$. Remarkably, the BTDF does not obey reciprocity as defined above.

1.3 Basic Reflection Models

Reflection from surfaces can be split into four broad categories: diffuse, glossy specular, perfect specular, and retro-reflective. Most real surfaces exhibit reflection that is a mixture of these four types.

• Diffuse surfaces scatter light equally in all directions. A perfectly diffuse surface isn’t physically realizable

  e.g. dull chalkboards, matte paint (near-diffuse surfaces).

• Glossy specular surfaces scatter light preferentially in a set of reflected directions—they show blurry reflections of other objects.

  e.g. plastic, high-gloss paint

• Perfect specular surfaces scatter incident light in a single outgoing direction.

  e.g. mirrors, glass

• Retro-reflective surfaces scatter light primarily back along the incident direction.

  e.g. velvet, the Earth’s moon

It is common to split BRDF into diffuse, specular and glossy components:

2. Geometry of BSDF

Reflection computations are evaluated in the shading coordinate system, which is defined by the orthonormal basis vectors $tangent$, $bitangent$, $normal$ aligned with the $x$, $y$ and $z$ axes, respectively. Directions vectors $\omega$ in world space are transformed into the shading coordinate system before any of the BRDF or BTDF methods are called.

Given a direction vector $\omega$, it is easy to compute cosine and sine of angles in the above image, for example:

$cos\theta = (normal \cdot \omega) = ((0, 0, 1) \cdot \omega) = \omega_z$

2.1 Transform vectors between world and local

Given vectors $tangent$, $bitangent$, $normal$ in world space, the matrix $M$ that transforms vectors from the world coordinate to the local coordinate is:

$ M = \begin{bmatrix} & tangent.x & tangent.y & tangent.z \newline & bitangent.x & bitangent.y & bitangent.z \newline & normal.x & normal.y & normal.z \end{bmatrix} = \begin{bmatrix} tangent \newline bitangent \newline normal \end{bmatrix} = \begin{bmatrix} t \newline b \newline n \end{bmatrix}$

It’s easy to verify the correctness of $M$: $Mn = (t \cdot n, b \cdot n, n \cdot n)$, because $t\perp n$ and $b \perp n$, and $n$ is normalized so $n \cdot n = 1$. Therefore, $Mn = (0, 0, 1) = n$, as expected.

The transposed matrix $M^T$ can take vectors back from the local coordinate to the world coordinate.

2.2 Geometric Normal VS Shading Normal

Geometric normal $n_g$ is defined by the surface geometry, i.e., it’s the normal of a triangle of the mesh, while shading normal $n_s$ is given by per-vertex normals or bump mapping (for more information please refer this answer on Stack Overflow).

3. Implementation of BSDF

3.1 The Interface of BSDF: BxDF

BRDFs and BTDFs share a common base class, BxDF, which describes a specific way to scatter light. Each BxDF has a BxDFType member, which holds flags representing categories of reflection and/or transmission this BxDF has, and the flags should have at least one of BSDF_REFLECTION or BSDF_TRANSMISSION set and exactly one of the diffuse, glossy, and specular flags.

Key class member functions (please refer to bsdf.cpp for more implementation details):

• BxDF::f()

  Returns the value of the distribution function for the given pair of directions. It’s a pure virtual function in the implementation.

  In addition, not all BxDFs can be evaluated with the f() method, perfectly specular objects only scatter light from a single incident direction into a single outgoing direction. Such BxDFs are best described with delta distributions that are zero except for the single direction where light is scattered.

• BxDF::Sample_f()

  Computes the direction of incident light $\omega_i$ given an outgoing direction $\omega_o$, and returns the value of the bidirectional scattering distribution for the chosen direction as well as the sampled direction and pdf.

  The default implementation of Sample_f() generates a uniformly random sample as the incident direction $\omega_i$. However, for delta distributions, Sample_f() has to choose a specific incident light direction.

3.2 The BSDF Class

The BSDF class represents a collection of BRDFs and BTDFs. The BSDF class holds a set of BxDF whose contributions are summed to give the full scattering function.

Key class member functions (please refer to bsdf.cpp for more implementation details):

• BSDF::f()

  Computes the f() of all of the matched BxDFs belonging to this BSDF, and returns the sum of these f()s.

  In details, first convert the given incident direction $\omega_i$ and the outgoing direction $\omega_o$ from world space to local space, and then use the local $\omega_i$ and $\omega_o$ to determine whether they are in the same hemisphere when computing f().

• BSDF::Pdf()

  Computes the average probability density function (pdf) of all BxDFs that match the given BxDFType.

• BSDF::Sample_f()

  Use the given random number to select one of the BxDFs which matches the given BxDFType flags. Then, sample an incident direction $\omega_i$ with the BxDF::Sample_f() of the selected BxDF. Finally, use BSDF::f() and BSDF::Pdf() to compute the total value of BSDF and average pdf of the sampled $w_i$.

Where to use BSDF?

The surface shader is represented by an instance of the Material interface class, which has a method that takes a point on a surface and creates a BSDF object that represents scattering at the point.

Determine reflection or transmission when evaluating the BSDF

If $w_i$ and $w_o$ lie in the same hemisphere with respect to the geometric normal, we evaluate the BRDFs, and otherwise we evaluate the BTDFs. $\omega_i$ and $\omega_o$ lies in the same hemisphere if $(\omega_i \cdot n_g) * (\omega_o * n_g) > 0$ ($\omega_i, \omega_o, n_g$ are vectors in the world space).

References

• Matt Pharr, Wenzel Jakob, and Greg Humphreys. Physically Based Rendering: From Theory To Implementation

• https://en.wikipedia.org/wiki/Bidirectional_scattering_distribution_function