Binary Lifting
Binary Lifting is a fabulous technique which can take $O(logn)$ time to find the lowest common ancestor (LCA) of two nodes in a tree, or to find the k-th ancestor of any node in a tree, based on a dynamic programming step to do some preprocessing. Besides, this technique can also be used to compute functions such as minimum, maximum and sum between two nodes of a tree in logarithmic time.
1. Preprocessing Using DP
We will first precompute a memo $dp$ to record the ancestors of a give node, based on dynamic programming. Assume there are $n$ nodes in the tree, then $0 \le i < n$ and $0 \le j < \lceil log_2(n) \rceil$, given a array $parent$ which store the parent of each node, here is the the optimal substructure:
\[dp[i][j] = \begin{cases} parent[i] \qquad & \text{if } j == 0 \newline \newline dp[dp[i][j - 1]][j - 1] \qquad & \text{else} \end{cases}\]where $dp[i][j]$ represent the $2^{j}$th ancestor of the node $i$. For example, the $1$st ancestor of node $6$ is $dp[6][0]$, apparently, $2^ 0 = 1$ and it is definite that the first ancestor of a given node is its parent. The optimal substructure exhibits the great feature of Binary Lifting, which breaks down the path between a node and its ancestor into two parts. The following example shows more details: the 4th ($2^2$) ancestor of node $5$ is the same as the 2nd ($2^1$) ancestor of the node $3$.
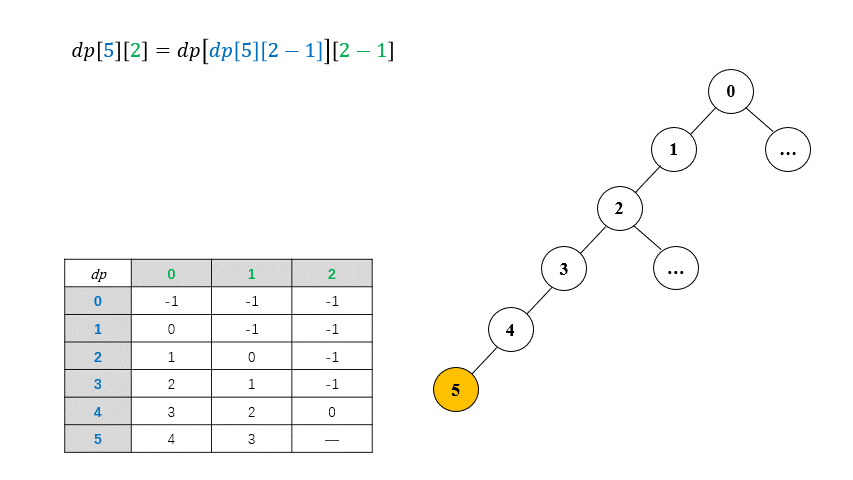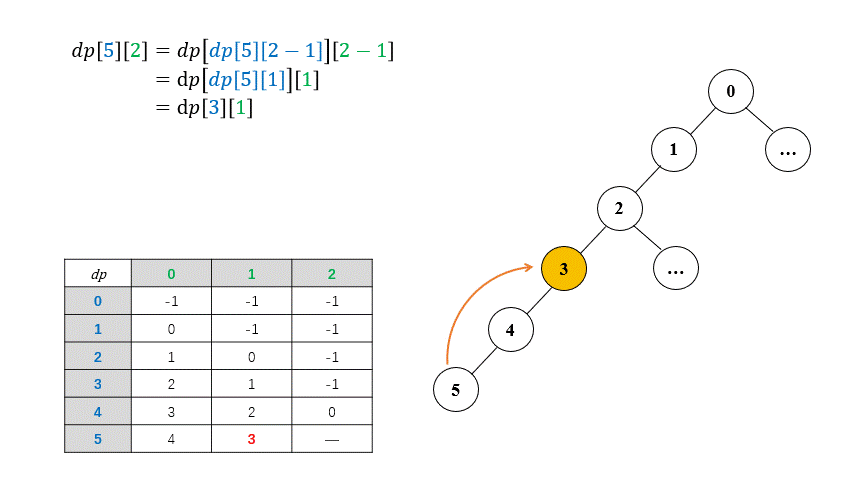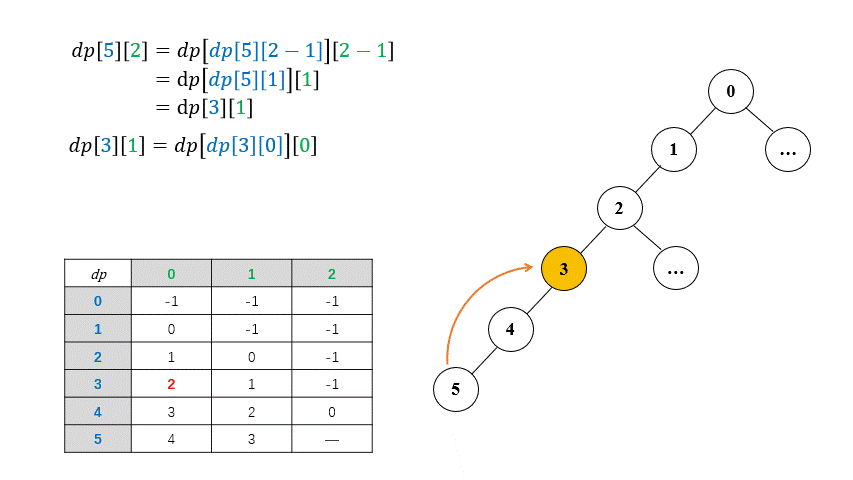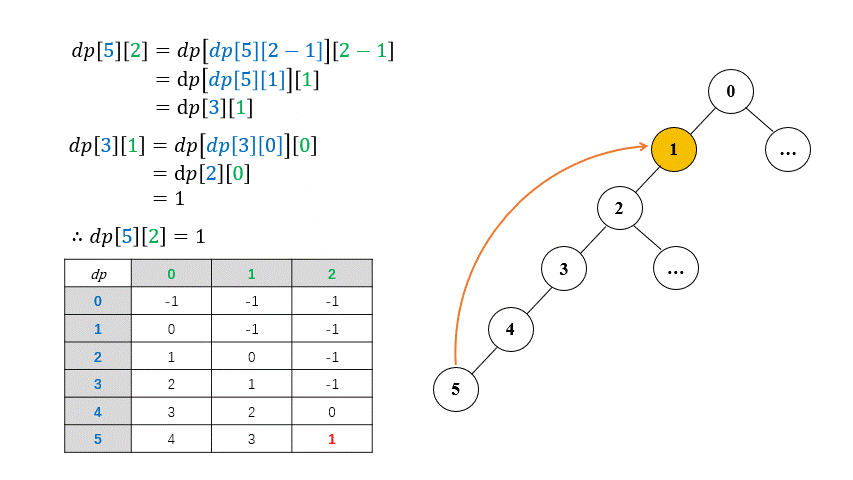
To be specific, the $2^{j}$th ancestor of the node $i$ is equal to the $2^{j - 1}$th ancestor of the node which $dp[i][j - 1]$ represents, and $dp[i][j - 1]$ represents the $2^{j - 1}$th ancestor of the node $i$. Thus, the $2^{j}$th ancestor of the node $i$ is namely the $2^{j - 1}$th ancestor of the $2^{j - 1}$th ancestor of the node $i$. If we calculated $2^{j-1}$ th ancestor of every node beforehand, it’s easy to calculate $2^j$ th ancestor based on the pre-computation.
The time complexity of the preprocessing is $O(nlogn)$.
2. Application
2.1 [LeetCode] 236. Lowest Common Ancestor of a Binary Tree
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
In general, this problem can be easily solved by a recursive approach which takes $O(n)$ time, because we are given the root of the tree and two nodes to find their LCA, so it’s unnecessary to spend extra $O(nlogn)$ time on preprocessing. However, when an array $parent$ is given instead of the root, binary lifting is absolutely a better choice.
The specific steps of the solution based on Binary Lifting:
- First, preprocess to compute the array $dp$ and an additional array $level$ where $level[i]$ represents the current depth of the node $i$ in a tree.
- Second, for given nodes $i$ and $j$, assume $level[i] > level[j]$, if not, just swap $i$ and $j$. This assumption means that the node $i$ is farther away from the root than the node $j$. Then find the ancestor of $i$ and set it as $i’$, which has the same level as $j$.
- If $i’ == j$, then $j$ is the LCA of the node $i$ and $j$.
- Otherwise, for both $i’$ and $j$, do the binary lifting to jump along the path from current level to the root, until one of them reach a node $k$, which is not LCA of $i$ and $j$, while the parent of $k$, $dp[k][0]$ is, and return $dp[k][0]$ as the LCA.
2.2 [LeetCode] 1483. Kth Ancestor of a Tree Node
You are given a tree with n nodes numbered from $0$ to $n - 1$ in the form of a parent array where $parent[i]$ is the parent of node $i$. The root of the tree is node $0$. Implement a function to return the k-th ancestor of the given node. If there is no such ancestor, return -1.
Any number can be expressed as the sum of powers of 2. For example, the binary number of $6$ is $0110$, so to find the 6th ancestor of a node $i_1$, we can first search for its 2nd ($2^1$) ancestor $i_2$. Then, search for the 4th ($2^2)$ ancestor of the node $i_2$, and set this node as $i_3$. Obviously, $6 = 2^2 + 2^1 = 4 + 2$, and $i_3$ is the 6th ancestor of the node $i_1$. This approach jumps fast to search for the desired ancestor, which take $O(logn)$ time.
class TreeAncestor
{
private:
vector<vector<int>> dp;
int log;
public:
TreeAncestor(int n, vector<int>& parent)
: log(ceil(log2(n)))
{
dp = vector<vector<int>>(n, vector<int>(log));
// Preprocessing:
for (int i = 0; i < n; i++)
{
dp[i][0] = parent[i];
for (int j = 1; j < log; j++)
{
if (dp[i][j - 1] == -1)
dp[i][j] = -1;
else
dp[i][j] = dp[dp[i][j - 1]][j - 1];
}
}
}
int getKthAncestor(int node, int k)
{
for (int j = 0; j < log; j++)
{
if ((k >> j) & 1) // the bit in the end is 1
{
node = dp[node][j];
if (node == -1)
break;
}
}
return node;
}
};
References
-
https://www.geeksforgeeks.org/lca-in-a-tree-using-binary-lifting-technique/
-
https://iq.opengenus.org/binary-lifting-k-th-ancestor-lowest-common-ancestor/
-
https://leetcode.com/problems/kth-ancestor-of-a-tree-node/discuss/686362/JavaC%2B%2BPython-Binary-Lifting