KMP Algorithm

The Knuth–Morris–Pratt (KMP) algorithm is a string-searching algorithm. It can search for occurrences of a word within a main string by employing the observation that when a mismatch occurs, the word itself embodies sufficient information to determine where the next match could begin, thus bypassing re-examination of previously matched characters. The time complexity of KMP algorithm is $O(n)$ in the worst case.

1. The Naive String Matching Algorithm

The problem: given a pattern with the length $m$ and a text with the length $n$, both of them are strings, then determine whether the pattern appears somewhere in the text.

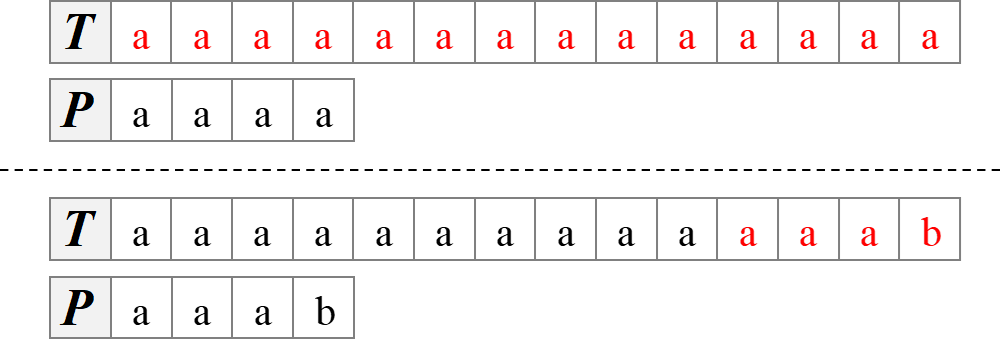
This brute-force algorithm takes time $O((n - m + 1)m)$, and this bound is tight in the worst case. Here are two worst cases:

2. Details of the Algorithm

2.1 The Auxiliary Table $\pi$ for the Pattern

The table $\pi$ for a pattern encapsulates knowledge about how the pattern matches against shifts of itself: it tells us the the number of characters which can be skipped, so that we can take advantage of this information to avoid testing useless shifts in the naive string matching algorithm.

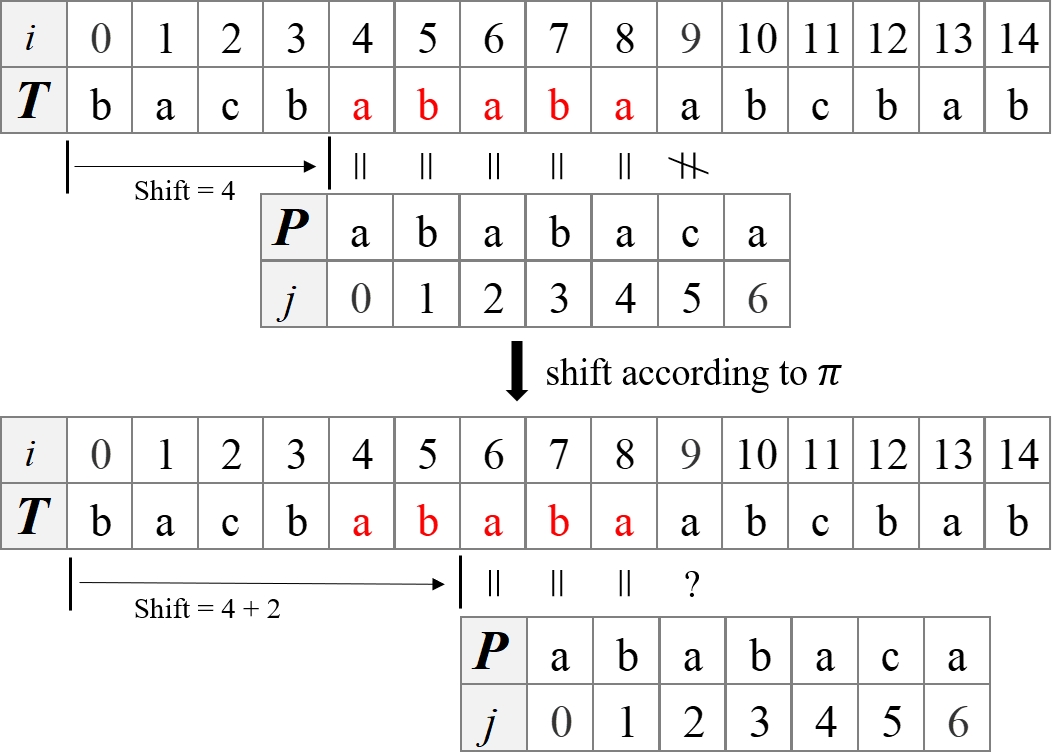
Given a text $T$ = “bacbababaabcbab” and a pattern $P$ = “ababaca”, after comparing $T[8]$ and $P[4]$, we have gotten 5 successfully matched characters, but the next character, $P[5]$, of the pattern fails to match the corresponding character of the text. If we use the naive string matching algorithm, we have to go back to the first character of $P$ and compare $P[0]$ and $T[5]$. However, we can just jump ahead to compare $P[3]$ and $T[9]$ and don’t need to consider $P[0…2]$, if we preprocess the pattern and obtain a table $\pi$.

Notation & Definition:

• Proper prefix: All the characters in a string, with one or more cut off the end. “a”, “ap”, “app” and “appl” are all the proper prefixes of “apple”.

• Proper suffix: All the characters in a string, with one or more cut off the beginning. “each”, “ach”, “ch” and “h” are all the proper suffixes of “peach”.

• $\pi[i]$: the length of the longest proper prefix of the pattern $P$ that is a proper suffix of $P[0… i]$. The following figure shows an example: $\pi[7] = 3$, because the proper suffix of $P[0…7]$ = “abcdeabc” is “abc”, which is also the longest proper prefix of $P$.

More examples:

2.2 Preprocess the Pattern to Compute $\pi$

We can precompute the necessary information by comparing the pattern against itself. To do that, we declare the variable $len$ keep track of the length of the longest proper prefix which is also a proper suffix. Note that $len$ not only represent the length of the successfully matched sub-pattern, it is also equal to the index of the character to be checked.

• Always initialize $\pi[0] = 0$, and set $len = 0$;

• Declare $i$ as the index of the currently processed character, $1 \le i \le (n - 1)$, then iterate the pattern from $P[1]$ to $P[n - 1]$.

  • When $P[i] == P[len]$, obviously, we can increase the length of the currently longest proper prefix to $len + 1$, so increase $len$ by one, then set $\pi[i] = len$, and do $i++$ to compare the next character.

  • Otherwise,

    \[\begin{cases} len = \pi[len - 1]; &\text {if } len > 0 \newline i++; \quad \text{// now len == 0} &\text {else} \end{cases}\]

A detailed and complete process of computing $\pi$:

Taking the pattern $P$ = “ababaca” as an example: $\pi[0] = 0$, $len = 0$

• $i = 1$, $P[0…1]$ = “ab”

  The proper prefix of “ab”: “a”

  The proper suffix of “ab”: “b”

  There are no matches, so $len = 0$, $\pi[1] = 0$.

• $i = 2$, $P[0…2]$ = “aba”

  The proper prefix of “aba”: “a” and “ab”

  The proper suffix of “aba”: “ba” and “a”

  We can find “a” is the longest proper prefix and the longest proper suffix of $P[0…2]$, so $len = 1$, $\pi[2] = 1$.

• $i = 3$, $P[0…3]$ = “abab”

  The proper prefix of “abab”: “a”, “ab” and “aba”

  The proper suffix of “abab”: “bab”, “ab” and “b”

  We can find “ab” is the longest proper prefix and the longest proper suffix of $P[0…3]$, so $len = 2$, $\pi[3] = 2$.

• $i = 4$, $P[0…4]$ = “ababa”

  The proper prefix of “ababa”: “a”, “ab”, “aba” and “abab”

  The proper suffix of “ababa”: “baba”, “aba”, “ba” and “a”

  Both “a” and “aba” are proper prefixes and suffixes, but “aba” is the longest one, so $len = 3$, $\pi[4] = 3$.

• $i = 5$, $P[0…5]$ = “ababac”

  Because each suffix ends with the character “c”, which don’t exist in any prefixes, so $len = 0$, $\pi[5] = 0$.

• $i = 6$, $P[0…6]$ = “ababaca”

  The proper prefix of “ababaca”: “a”, “ab”, “aba”, “abab”, “ababa”, “ababac”

  The proper suffix of “ababaca”: “babaca”, “abaca”, “baca”, “aca”, “ca”, “a”

  We can find “a” is the longest proper prefix and the longest proper suffix of $P[0…6]$, so $len = 1$, $\pi[6] = 1$.

Why use $len = \pi[len - 1]$?

• Actually, when $P[i] \ne P[len]$, directly setting $len = 0$ and $\pi[i] = 0$ can solve most of situations:

  • $P$ = “abcd”, $i = 3$, $len = 0$

    Set $\pi[3] = 0$, or we can just ignore computing $\pi[3]$ if we initialize $\pi$ as an array of zeros.

  • $P$ = “ababaca”, $i=5$, $len = 3$

    At first, $len = \pi[len - 1] = \pi[2] = 1$, but still $P[i] \ne P[len]$,

    then, $len = \pi[len - 1] = \pi[0] = 0$. At this time, all the proper prefixes of $P[0…5]$ = “ababac” cannot match a proper suffix, so apparently $\pi[5] = 0$

• A special case will be taken into account due to $len = \pi[len - 1]$:

  $P$ = “aaabaaaaa”, $i=7$, $len = 3$

  Because $P[7]$ = “a”, $P[3]$ = “b”, so $P[i] \ne P[len]$ at this time. Set $len = \pi[len - 1] = \pi[2] = 2$, and we can find that $P[2] = P[7]$ so that set $\pi[7]$ = ++$len = 3$. In other words, “aaa” is both the longest proper prefix and the longest proper suffix of $P[0…7]$ = “aaabaaaa”.

2.3 How to Use $\pi$

We use the $\pi$ to decide the next characters to be matched. The idea is to not match a character that we know will anyway match.

Assume we are going to compare the $(i + 1)^{th}$ character $T[i]$ of the text and the $(j + 1)^{th}$ character $P[j]$ of the pattern.

• If $T[i] == P[j]$

  Match! Do $i$++ and $j$++ to compare the next character, and if $j == n$, we successfully find an appearance of the pattern in the text.

• Else, $T[i] \ne P[j]$

  Use $\pi$ to find the next character in $P$ to be compared with $T[i]$. Because we have successfully matched the previous $j$ characters, i.e., $P[0…\ (j - 1)] = T[(i - j)…\ (i - 1)]$, and with the help of $\pi[j - 1]$ which represents the length of the longest proper prefix and proper suffix of $P[0…\ (j - 1)]$, set $k =\pi[j - 1]$ we can get the following equation:

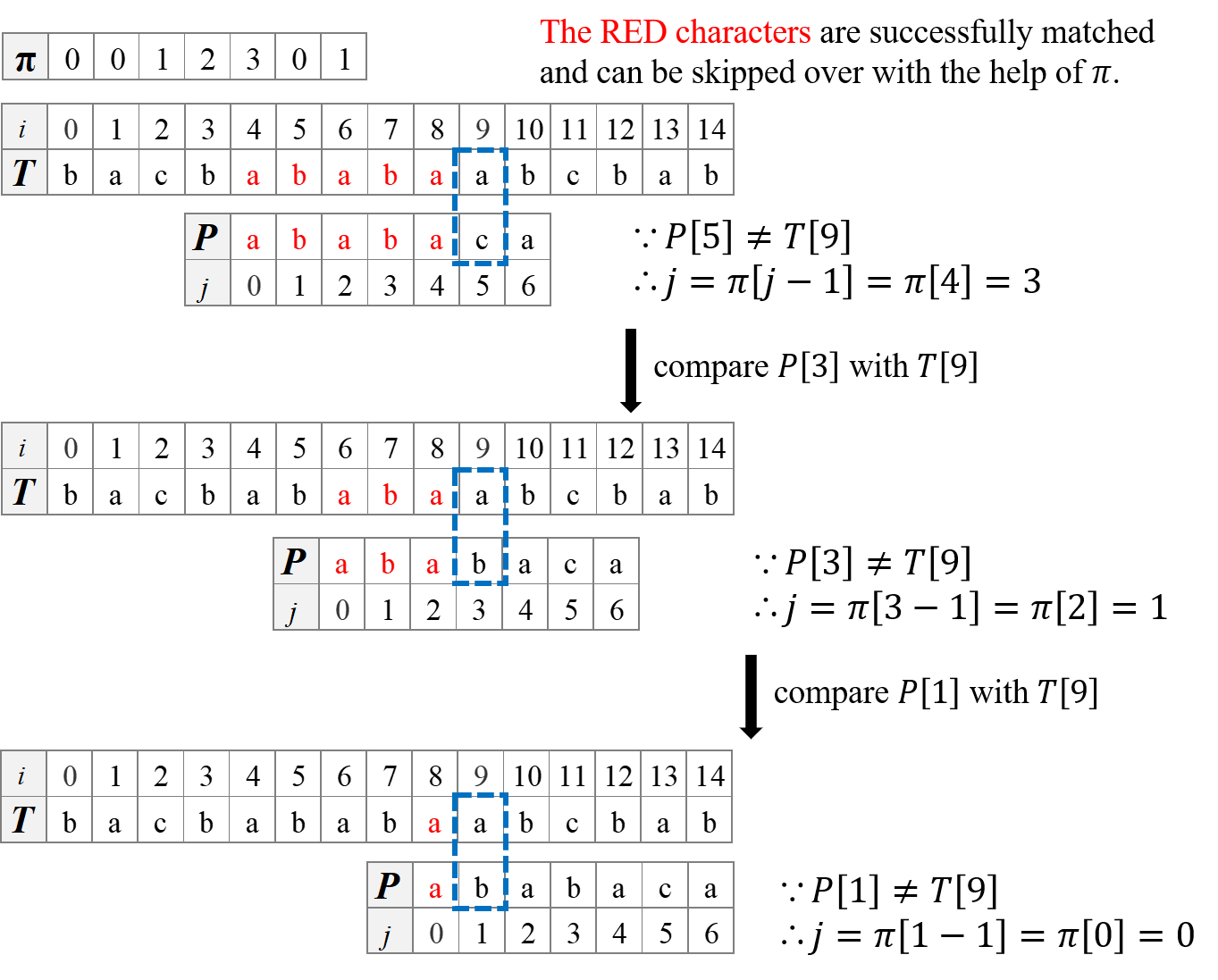
  \[\begin{aligned} P[0...\ (k - 1)] = P[(j - k)...\ (j - 1)] & \newline P[0...\ (j - 1)] = T[(i - j)...\ (i - 1)] \ \ \text{&&} \ \ k < j & \end{aligned} \Rightarrow P[0...\ (k - 1)] = T[(i - k)...\ (i - 1)]\]

  Thus, we can directly compare $P[k]$ and $T[i]$ to determine whether they match or not, so as to save the time of comparing the previous $\pi[j - 1]$ characters.

  Here is a concrete example:

  

3. Application

3.1 [LeetCode] 28. Implement strStr()

Implement strStr(). Return the index of the first occurrence of needle in haystack, or -1 if needle is not part of haystack.

class Solution
{
	vector<int> preprocess(const string& pattern)
	{
		int n = pattern.size();
		vector<int> pi(n);

		for (int i = 1, len = 0; i < n; )
		{
			if (pattern[i] == pattern[len])
			{
				pi[i++] = ++len;
			}
			else
			{
				if (len > 0)
					len = pi[len - 1];
				else
					i++;
			}
		}
		return pi;
	}

public:
	int strStr(string haystack, string needle)
	{
		if (needle.empty())
			return 0;

		vector<int> pi = preprocess(needle);
		int m = haystack.size();
		int n = needle.size();

		for (int i = 0, j = 0; i < m; )
		{
			if (haystack[i] == needle[j])
			{
				i++; j++;
			}
			else
			{
				if (j > 0)
					j = pi[j - 1];
				else
					i++;
			}

			if (j == n)
				return i - j;
		}

		return -1;
	}
};

3.2 [LeetCode] 214. Shortest Palindrome

Given a string s, you are allowed to convert it to a palindrome by adding characters in front of it. Find and return the shortest palindrome you can find by performing this transformation.

class Solution
{
	int preprocess(const string& s)
	{
		string temp = s + "#" + string(s.rbegin(), s.rend());
		vector<int> pi(temp.size());

		for (int i = 1, len = 0; i < temp.size(); )
		{
			if (temp[i] == temp[len])
			{
				pi[i++] = ++len;
			}
			else
			{
				if (len > 0)
					len = pi[len - 1];
				else
					i++;
			}
		}

		return pi.back();
	}
public:
	string shortestPalindrome(string s)
	{
		int max_palind_len = preprocess(s);
		string added_str = s.substr(max_palind_len);
		reverse(added_str.begin(), added_str.end());
		return added_str + s;
	}
};

References

• Thomas H. Cormen. Introduction to Algorithms - 3rd Edition

• https://www.geeksforgeeks.org/kmp-algorithm-for-pattern-searching/

• http://jakeboxer.com/blog/2009/12/13/the-knuth-morris-pratt-algorithm-in-my-own-words/