Manacher’s Algorithm

Manacher’s Algorithm is an amazing algorithm to solve the problem of longest palindromic substring in $O(n)$ time.

1. Longest Palindromic substring

Before we get started, I should mention that there are another two easier approaches to solve [LeetCode] 5. Longest Palindromic Substring, they are dynamic programming approach and expand around center approach, however, both of them take $O(n^2)$ time, so there is no doubt that Manacher’s Algorithm is the optimized solution.

2. Details of the Algorithm

2.1 Algorithm’s Objective

Given a string $S$ with a size of $n$, the objective of Manacher’s Algorithm is to build a table $p$ such that knowing the value of $p[i]$ enables us to find the length of the longest palindromic substring with center at the position $i$.

2.2 Preprocess

Because a palindromic substring can have a center located at a single character or have a center located at a pair of characters, there may have a problem of locating the center: at a specific index or between two indexes.

To avoid this problem and for convenience, insert an arbitrary character, which doesn’t appear in the string, like ‘#’, in the beginning and end of $S$ and between every two characters of $S$, so that to form a new string $S’$. Also, we can prepend and append another arbitrary character after inserting ‘#’ (such as ‘\$’ and ‘@’ in the following example), to avoid bounds checking, but these two characters, ‘\$’ and ‘@’, will not be considered when running the algorithm.

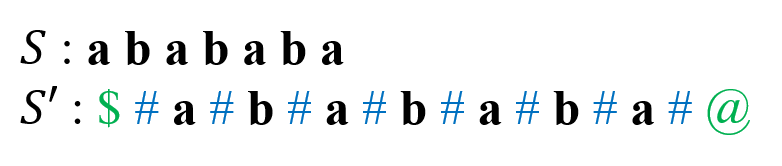
We can observe that, if the palindromic substring with a length $n_i$ in $S$, it has a corresponding palindromic substring with a length $2n_i + 1$ in $S’$. In general, every palindromic substring in the original string corresponds to a palindromic substring in the transformed string of the odd length.

2.3 Explanation for $p[i]$

$p[i]$ represents the radius of the largest odd-length palindromic substring centered at index $i$.

2.4 Variables Declaration

• $c$ : the center of the currently known palindromic substring with a right boundary which is the closest to the end of the transformed string $S’$.
• $r$ : the rightmost boundary of the palindromic substring centered at $c$. So current $c + r$ can return the max index among all the known palindromic substrings.
• $i$ : the position of a character in $S’$ whose palindromic span is being determined, and $i$ is alway to the right of $c$.
• $Palind(j)$ : the palindromic substring centered at the position $j$.

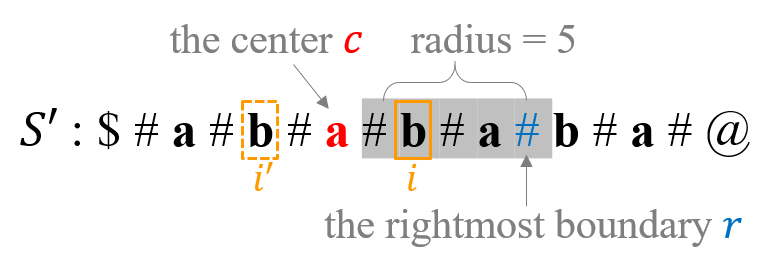
Let $i’$ be the mirrored position of $i$ with respect to the center $c$, and $i’$ and $i$ has such a relation:

\[i - c = c - i' \ \Leftrightarrow \ i' = 2c - i\]

2.5 How to Compute $p[i]$?

Assume that $p[i’]$ for all $i’ < i$ has already been calculated, and then iterate $i$ from $1$ to $n - 2$ to determine the value of $p[i]$, where $n$ is the size of the transformed string $S’$, ignoring the beginning ‘$’ and the end ‘@’.

There are 3 cases when determining $p[i]$:

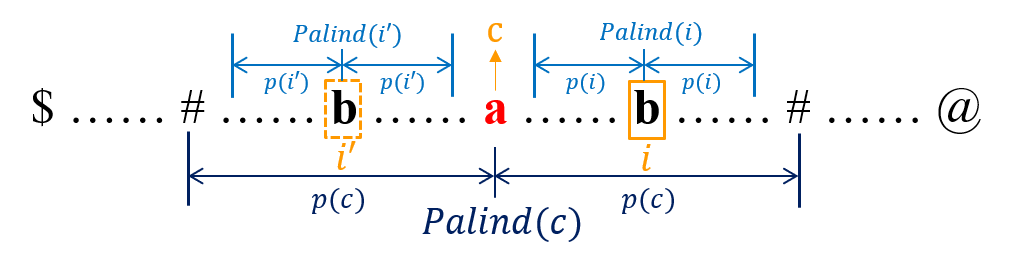
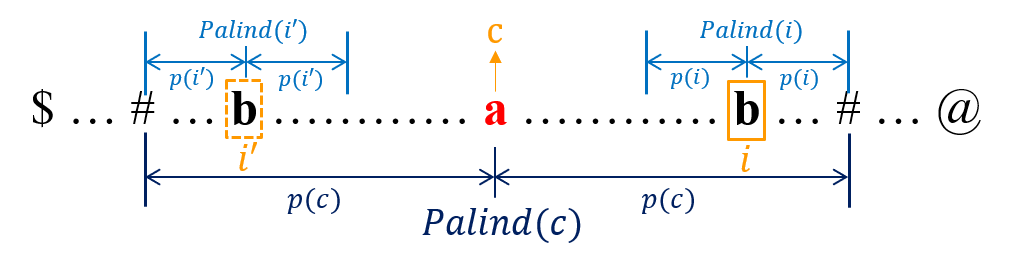
• Case 1: $Palind(i’)$ is totally within the range of $Palind(c)$, as shown below. According to the mirrored property of the palindrome, we can get that p[i] = p[i']. For example, $S$ = “abababa”, $S’$ = “\$#a#b#a#b#a#b#a#@”, $c = 6$, $i = 8$.

• Case 2: There exists a part of $Palind(i’)$ outside $Palind(c)$, i.e., $Palind(i’)$ extends beyond the left boundary of $Palind(c)$. We can get that p[i] = r - i. For example, $S$ = “ecbceaecbcg”, $S’$ = “\$#e#c#b#c#e#a#e#c#b#c#g#@”, $c = 12$, $i = 18$.

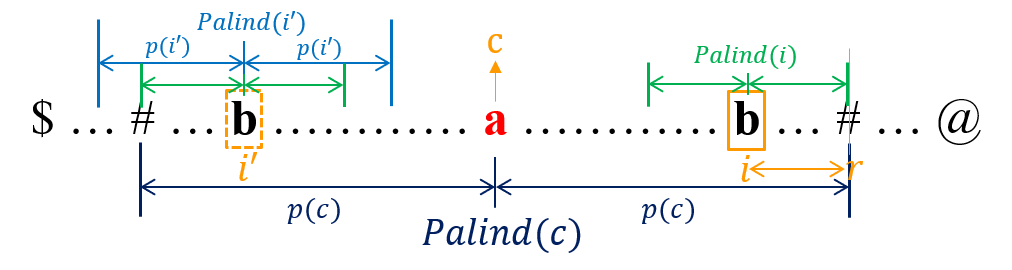
It is impossible to make the value of $p[i]$ larger, i.e., to extend $Palind(i)$ beyond $r$. Assume that we add a short substring with the length $l$ to the beginning and end of $Palind(i’)$ and $Palind(i)$, then the longest palindromic substring centered at $c$ should have a radius $p(c) + l$, which contradicts with the assumption.

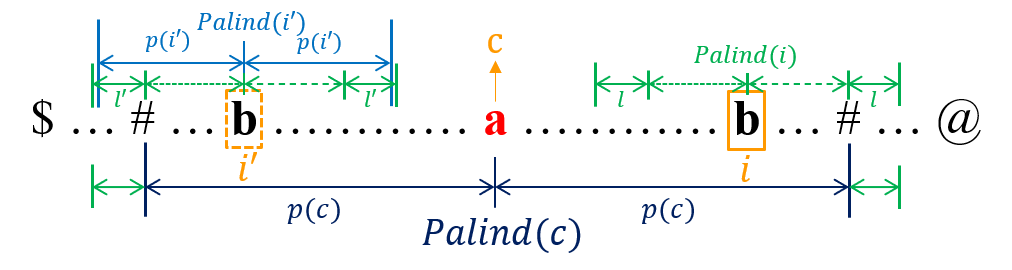
• Case 3: The left boundary of $Palind(i’)$ is the same as the left boundary of $Palind(c)$. At this time , according to results we got from Case 1 and Case 2, $p[i]$ may be equal to $p[i’]$ or be equal to $r - i$. For example, $S$ = “cbceaecbceaec”, $S’$ = “\$#c#b#c#e#a#e#c#b#c#e#a#e#c#@”, $c = 10$, $i = 16$. Besides, we are not sure whether we can continue to increase $p[i]$, so we just try to extend the right boundary of $Palind(i)$ while $S’[i - (p[i] + 1)] == S’[i + (p[i] + 1)]$.

Update the center $c$ and the rightmost boundary $r$ during the above iteration when reaching a righter boundary index.

3. Implementation of the Algorithm

string preprocess(string& s)
{
    string new_s(2 * s.size() + 3, '#');
    new_s[0] = '$';
    new_s.back() = '@';

    for (int i = 0; i < s.size(); i++)
    {
        new_s[2 * i + 2] = s[i];
    }
    return new_s;
}

string longestPalindrome(string s)
{
    if (s.empty())
        return "";

    s = preprocess(s);
    vector<int> p(s.size());
    int c = 0;
    int r = 0;
    int max_c = 0;  // the center of the currently known longest palindromic substring

    for (int i = 1; i < s.size() - 1; i++)
    {
        // Case 1 and Case 2
        if (i < r)  
            p[i] = min(p[2 * c - i], r - i);

        // Case 3
        while (s[i - (p[i] + 1)] == s[i + (p[i] + 1)])
            p[i]++;

        // Update when reaching a righter boundary index
        if (i + p[i] > r)
        {
            c = i;
            r = i + p[i];
        }

        // Find a longer palindromic substring
        if (p[max_c] < p[i])
            max_c = i;
    }

    // Get the center index of the longest palindromic substring of the orginal string s
    int center = ceil(double(max_c - 2) / 2);  
    return s.substr(center - p[max_c] / 2, p[max_c]);
};

4. Other Approaches to Find the Longest Palindromic substring

4.1 Dynamic Programming

string longestPalindrome(string s)
{
    string max_palind;
    int n = s.size();
    vector<vector<bool>> dp(n, vector<bool>(n));

    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
        {
            if (s[j] == s[i] && (j + 1 >= i - 1 || dp[j + 1][i - 1]))
            {
                dp[j][i] = true;
                if (max_palind.size() < i - j + 1)
                {
                    max_palind = s.substr(j, i - j + 1);
                }
            }
        }
    }

    return max_palind;
}

4.2 Expand Around Center

int expandAroundCenter(const string& s, int left, int right)
{
    while (left >= 0 && right < s.size() && s[left] == s[right])
    {
        left--;
        right++;
    }

    return right - left - 1;
}

string longestPalindrome(string s)
{
    string max_palind = "";
    for (int i = 0; i < s.size(); i++)
    {
        int len1 = expandAroundCenter(s, i, i);
        int len2 = expandAroundCenter(s, i, i + 1);
        int max_len = max(len1, len2);
        if (max_len > max_palind.size())
        {
            int start = i - (max_len - 1) / 2;
            max_palind = s.substr(start, max_len);
        }
    }

    return max_palind;
}

References

• https://www.hackerrank.com/topics/manachers-algorithm

• https://ethsonliu.com/2018/04/manacher.html